Statistik memiliki banyak aplikasi dalam pengumpulan data, baik dalam skala kecil maupun besar. Salah satu rumus yang bisa Anda gunakan yaitu simpang kuartil.
Ukuran letak data terdiri dari beberapa sub kategori, dan salah satunya adalah kuartil, desil, dan persentil. Kali ini, kita akan membahas khusus tentang simpang kuartil.
Pengertian Simpang Kuartil

Kuartil adalah nilai yang membagi data berurutan menjadi empat bagian yang memiliki jumlah data yang sama.
Dalam konteks ini, terdapat tiga kuartil utama: kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3).
Pertanyaannya adalah, apa hubungan antara kuartil dan simpangan? Kuartil adalah salah satu jenis ukuran letak data, sementara simpang kuartil adalah ukuran penyebaran data.
Istilah ini juga disebut jangkauan semi antar kuartil, setara dengan setengah dari jangkauan antar kuartil. Dalam istilah lain, dapat disebut sebagai deviasi kuartil atau rentang semi-interkuartil.
Seperti yang kita ketahui, jangkauan antar kuartil adalah selisih antara kuartil atas dan kuartil bawah. Oleh karena itu, untuk menghitung simpangan kuartil, kita perlu menentukan nilai kuartil atas dan kuartil bawah.
Simpangan ini berguna untuk mengukur jarak antara kuartil kedua (Q2) dengan kuartil pertama (Q1) atau kuartil ketiga (Q3).
Penting untuk diingat bahwa nilai rata-rata jarak ini dapat bervariasi tergantung pada distribusi data.
Cara Mencari Simpang Kuartil

Proses mencari simpang kuartil adalah suatu tugas yang relatif sederhana, tergantung pada jenis data yang ada, baik itu data tunggal atau data berkelompok.
Data tunggal adalah data yang terdiri dari satu jenis data tunggal, sedangkan data berkelompok mencakup rentang data atau data dalam kelompok tertentu.
Meskipun prinsip dasar dalam mencari simpangan tetap sama, ada sedikit perbedaan dalam pendekatannya tergantung pada jenis data yang digunakan.
Langkah-langkah untuk mencari simpang kuartil adalah sebagai berikut:
Mengurutkan Data
Langkah pertama dalam mencari simpang kuartil adalah mengurutkan data dalam urutan yang berurutan, dari nilai terkecil hingga terbesar.
Dengan mengurutkan data ini, kita dapat dengan mudah menemukan nilai kuartil atas, kuartil bawah, dan kuartil tengah.
Ketika data telah diurutkan, kita dapat melanjutkan ke langkah-langkah berikutnya.
Membagi Data Menjadi 3 Bagian yang Sama
Dalam kasus data tunggal, membagi data menjadi tiga bagian yang sama relatif mudah. Namun, dalam data berkelompok, kita perlu menggunakan rumus khusus untuk menemukan pembagian ini.
Untuk memahami lebih lanjut, kita akan memberikan contoh kasus nanti.
Menghitung Jangkauan Antar Kuartil
Jangkauan antara kuartil dapat dihitung dengan mengurangkan nilai kuartil atas (Q3) dengan nilai kuartil bawah (Q1).
Hasil pengurangan ini adalah jangkauan antara kuartil. Menghitungnya cukup sederhana.
Menentukan Simpangan Kuartil
Setelah kita memiliki jangkauan antara kuartil, kita dapat dengan mudah menghitung simpang kuartil.
Caranya adalah dengan mengalikan jangkauan antara kuartil dengan koefisien 0,5 atau ½ sesuai dengan rumus yang telah diberikan sebelumnya.
Contoh Soal dan Cara Penyelesaiannya
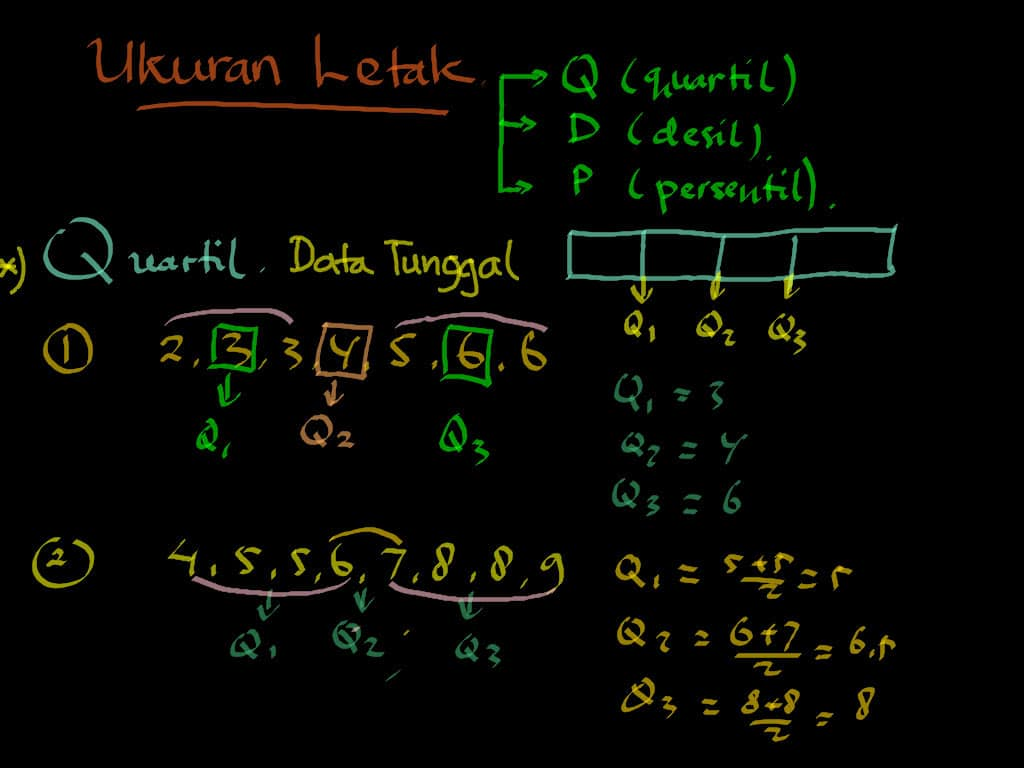
Rumus jangkauan antar kuartil digunakan untuk mengukur selisih antara nilai kuartil atas (Q3) dan kuartil bawah (Q1).
Untuk menghitungnya, terlebih dahulu kita harus menentukan nilai Q1, Q2, dan Q3 dari data tersebut.
Rumus simpang kuartil adalah alat yang berguna untuk mengetahui seberapa tersebarnya data di sekitar kuartil tengah (Q2).
Rumus ini dapat diterapkan pada data tunggal dengan mudah. Langkah mengukur jarak antara Q1 dan Q3. Ini adalah nilai yang berguna dalam mengidentifikasi sebaran data di antara kuartil.
Rumus pagar mengukur batas atas (Pagar luar) dan batas bawah (Pagar dalam) dari data.
Pagar luar adalah Q3 ditambah dengan langkah, sedangkan pagar dalam adalah Q1 dikurangi dengan langkah.
Contoh soal simpangan kuartil
Mari kita terapkan rumus-rumus ini pada contoh soal berikut ini dengan data tunggal: 6, 6, 7, 9, 13, 16, 20.
Penjelasan jawaban
Untuk menghitung jangkauan (J), kita mengurangkan data terbesar dengan data terkecil:
J = 20 – 6 = 14
Untuk menghitung jangkauan antar kuartil (H), pertama-tama kita harus menentukan Q1, Q2, dan Q3:
Q1 = 6
Q2 = 9
Q3 = 16
H = Q3 – Q1 = 16 – 6 = 10
Simpangan kuartil (Qd) dapat dihitung dengan rumus:
Qd = ½ H = ½ × 10 = 5
Langkah (L) dihitung dengan rumus:
L = 3/2 H = 3/2 × 10 = 15
Pagar dalam (Pd) dihitung dengan:
Pd = Q1 – L = 6 – 15 = -9
Pagar luar (Pl) dihitung dengan:
Pl = Q3 + L = 16 + 15 = 31
Dengan menggunakan rumus simpangan kuartil, kita dapat menganalisis data dengan lebih baik dan memahami sebaran dan karakteristiknya tanpa memberikan opini.
Tips Mudah Menghafalkan Rumus Matematika
Siswa perlu memahami metode menghafal rumus matematika agar mereka lebih siap menghadapi ujian.
Berikut adalah delapan cara menghafal rumus matematika yang dapat diterapkan.
Visualisasi Warna
Manusia memiliki dua otak, otak kanan yang cenderung pada imajinasi dan kreativitas, dan otak kiri yang lebih fokus pada logika.
Visualisasi yang jelas membantu dalam menyimpan informasi dengan cepat. Anda dapat menggabungkan kedua kemampuan otak ini dengan menggunakan visualisasi warna.
Gunakan lembar kosong dan spidol warna untuk menuliskan rumus matematika. Menggunakan warna-warna tertentu untuk mewakili setiap rumus akan mempermudah menghafalnya.
Familiarkan Otak dengan Rumus
Langkah selanjutnya adalah memfamiliarkan otak dengan rumus dan materi pelajaran. Sebelum memasuki pelajaran matematika, luangkan waktu untuk membaca topik yang akan dibahas.
Anda tidak perlu menghafal rumus pada awalnya, cukup luangkan waktu untuk memahami kontennya selama 5 menit.
Ini akan membantu Anda memahami materi secara keseluruhan dan mempermudah proses menghafal rumus di kemudian hari.
Memahami Makna Rumus
Jangan hanya mencoba menghafal rumus tanpa memahami maknanya. Ini hanya akan membuang waktu Anda dan mungkin menyebabkan kebingungan.
Memahami hubungan antara rumus dan maknanya penting. Cobalah menggambar diagram yang relevan dengan rumus yang Anda pelajari.
Ini bisa berupa parabola atau lingkaran, tetapi pastikan diagram tersebut terkait dengan rumus yang bersangkutan.
Praktek Aktif
Salah satu cara terbaik untuk menghafal rumus matematika adalah dengan praktek aktif. Cobalah untuk menyelesaikan berbagai soal matematika yang melibatkan rumus yang sedang Anda pelajari.
Praktek akan membantu Anda memahami cara mengaplikasikan rumus dalam berbagai konteks, sehingga Anda tidak hanya menghafal, tetapi juga memahami penggunaannya.
Sederhanakan Rumus
Kadang-kadang rumus matematika terlihat rumit. Cobalah untuk menyederhanakan rumus tersebut menjadi bentuk yang lebih mudah dipahami.
Ini dapat membantu mengingat rumus dengan lebih baik. Jika Anda memahami dasar-dasarnya, Anda akan lebih mudah mengingatnya.
Sama halnya dengan menerapkan rumus mean, median, modus.
Buat Catatan
Buat catatan atau ringkasan tentang rumus-rumus yang Anda pelajari. Catatan ini dapat membantu Anda mengulang rumus secara berkala dan mengingatnya dengan lebih baik.
Kelompokkan Rumus
Kategorikan rumus-rumus berdasarkan jenisnya. Misalnya, kelompokkan rumus-rumus trigonometri, geometri, atau aljabar.
Ini akan membantu Anda mengatur rumus-rumus secara lebih terstruktur.
Rumus simpang kuartil akan membantu Anda mendapatkan data yang berhubungan dengan data kelompok jadi lebih mudah.













